```{r setup, include=FALSE} knitr::opts_chunk$set(echo = FALSE) ``` ```{r, echo=F, message=F, warning=F} library(readr) library(openintro) library(here) library(tidyverse) library(xtable) data(COL) ``` # Comparing mean with ANOVA ## \centering {height="25%"} - The Wolf River in Tennessee flows past an abandoned site once used by the pesticide industry for dumping wastes, including chlordane (pesticide), aldrin, and dieldrin (both insecticides). \pause - These highly toxic organic compounds can cause various cancers and birth defects. \pause - The standard methods to test whether these substances are present in a river is to take samples at six-tenth depth. \pause - But since these compounds are denser than water and their molecules tend to stick to particles of sediment, they are more likely to be found in higher concentrations near the bottom than near mid depth. ## Data Aldrin concentration (nanograms per liter) at three levels of depth. \begin{center} \begin{tabular}{r | c | c} \hline & aldrin & depth \\ \hline 1 & \textcolor{gray}{3.80} & \textcolor{gray}{bottom} \\ 2 & \textcolor{gray}{4.80} & \textcolor{gray}{bottom} \\ ... & & \\ 10 & \textcolor{gray}{8.80} & \textcolor{gray}{bottom} \\ 11 & \textcolor{blue}{3.20} & \textcolor{blue}{middepth} \\ 12 & \textcolor{blue}{3.80} & \textcolor{blue}{middepth} \\ ... & & \\ 20 & \textcolor{blue}{6.60} & \textcolor{blue}{middepth} \\ 21 & \textcolor{green}{3.10} & \textcolor{green}{surface} \\ 22 & \textcolor{green}{3.60} & \textcolor{green}{surface} \\ ... & & \\ 30 & \textcolor{green}{5.20} & \textcolor{green}{surface} \\ \hline \end{tabular} \end{center} ## Exploratory analysis Aldrin concentration (nanograms per liter) at three levels of depth. ```{r, echo=F, message=F, warning=F,fig.width=5, fig.height=2,fig.align='center'} aldrin = read_csv("dataset/aldrin.csv") # dotplot par(mar=c(2,4.1,0,0), las=1, mgp=c(3,0.7,0), mfrow = c(3,1), cex.lab = 1.8, cex.axis = 2) dotPlot(aldrin$aldrin[aldrin$depth == "bottom"], xlim = c(3,9), axes = FALSE, col = COL[1,2], xlab = "", ylab = "bottom", cex = 3) dotPlot(aldrin$aldrin[aldrin$depth == "middepth"], xlim = c(3,9), axes = FALSE, col = COL[1,2], xlab = "", ylab = "middepth", cex = 3) dotPlot(aldrin$aldrin[aldrin$depth == "surface"], xlim = c(3,9), col = COL[1,2], ylab = "surface", cex = 3) ``` \begin{center} \begin{tabular}{l | c c c} & n & mean & sd \\ \hline bottom & 10 & 6.04 & 1.58 \\ middepth& 10 & 5.05 & 1.10 \\ surface & 10 & 4.20 & 0.66 \\ \hline overall & 30 & 5.1 0 & 1.37 \end{tabular} \end{center} ## Research question \alert{Is there a difference between the mean aldrin concetrations among the three levels?} \pause - To compare means of 2 groups we use a Z or a T statistic. \pause - To compare means of 3+ groups we use a new test called **ANOVA** and a new statistic called **F**. ## ANOVA ANOVA is used to assess whether the mean of the outcome variable is different for different levels of a categorical variable. \begin{itemize} \item[$H_0:$] The mean outcome is the same across all categories,\[\mu_1 = \mu_2 = \cdots = \mu_k, \] where $\mu_i$ represents the mean of the outcome for observations in category $i$. \item[] \item[$H_A:$] At least one mean is different than others. \end{itemize} ## Conditions \begin{enumerate} \item The observations should be independent within and between groups \begin{itemize} \item If the data are a simple random sample from less than 10\% of the population, this condition is satisfied. \item Carefully consider whether the data may be independent (e.g. no pairing). \item Always important, but sometimes difficult to check. \end{itemize} \pause \item The observations within each group should be nearly normal. \begin{itemize} \item Especially important when the sample sizes are small. \end{itemize} \alert{How do we check for normality?} \pause \item The variability across the groups should be about equal. \begin{itemize} \item Especially important when the sample sizes differ between groups. \end{itemize} \alert{How can we check this condition?} \end{enumerate} ## $z/t$ test vs. ANOVA - Purpose \begin{columns} \begin{column}{0.45\textwidth} \centering{$\mathbf{z/t}$ \textbf{test}} \raggedright Compare means from \textbf{two} groups to see whether they are so far apart that the observed difference cannot reasonably be attributed to sampling variability. \centering{$H_0: \mu_1=\mu_2$} \end{column} \begin{column}{0.45\textwidth} \centering{\textbf{ANOVA}} \raggedright Compare the means from \textbf{two or more} groups to see whether they are so far apart that the observed difference cannot all reasonably be attributed to sampling variability. \centering{$H_0: \mu_1=\mu_2= \cdots = \mu_k$} \end{column} \end{columns} ## $z/t$ test vs. ANOVA - Method \begin{columns} \begin{column}{0.45\textwidth} \centering{$\mathbf{z/t}$ \textbf{test}} \raggedright Compare a test statistic (a ratio). \centering{$z/t = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1-\mu_2)}{SE(\bar{x}_1-\bar{x}_2)}$} \end{column} \begin{column}{0.45\textwidth} \centering{\textbf{ANOVA}} \raggedright Compare a test statistic (a ratio). \centering{$F = \frac{\text{variability bet. groups}}{\text{variability w/in groups}}$} \end{column} \end{columns} \pause - Large test statistics lead to small p-values. - If the p-value is small enough $H_0$ is rejected, we conclude that the population means are not equal. ## $z/t$ test vs. ANOVA - With only two groups t-test and ANOVA are equivalent, but only if we use a pooled standard variance in the denominator of the test statistic. \pause - With more than two groups, ANOVA compares the sample means to an overall **grand mean**. ## Hypotheses \alert{What are the correct hypotheses for testing for a difference between the mean aldrin concentrations among the three levels?} \begin{enumerate}[(a)] \item $H_0: \mu_B = \mu_M = \mu_S$ \\ $H_A: \mu_B \ne \mu_M \ne \mu_S$ \\ \item $H_0: \mu_B \ne \mu_ M \ne \mu_S$ \\ $H_A: \mu_B = \mu_M = \mu_S$ \\ \item $H_0: \mu_B = \mu_M = \mu_S$ \\ $H_A:$ At least one mean is different. \item $H_0: \mu_B = \mu_M = \mu_S = 0$ \\ $H_A:$ At least one mean is different. \item $H_0: \mu_B = \mu_M = \mu_S$ \\ $H_A: \mu_B > \mu_M > \mu_S$ \\ \end{enumerate} ## Hypotheses \alert{What are the correct hypotheses for testing for a difference between the mean aldrin concentrations among the three levels?} \begin{enumerate}[(a)] \item $H_0: \mu_B = \mu_M = \mu_S$ \\ $H_A: \mu_B \ne \mu_M \ne \mu_S$ \\ \item $H_0: \mu_B \ne \mu_ M \ne \mu_S$ \\ $H_A: \mu_B = \mu_M = \mu_S$ \\ \item \alert{$H_0: \mu_B = \mu_M = \mu_S$} \\ \alert{$H_A:$ At least one mean is different.} \item $H_0: \mu_B = \mu_M = \mu_S = 0$ \\ $H_A:$ At least one mean is different. \item $H_0: \mu_B = \mu_M = \mu_S$ \\ $H_A: \mu_B > \mu_M > \mu_S$ \\ \end{enumerate} ## Test statistic \alert{Does there appear to be a lot of variability within groups? How about between groups?} \centering{$F = \frac{\text{variability bet. groups}}{\text{variability w/in groups}}$} 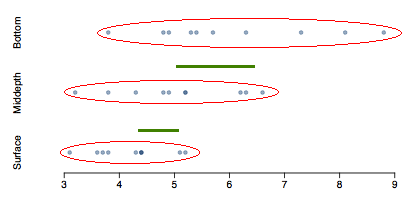{height="40%"} ## $F$ distribution and p-value \centering{$F = \frac{\text{variability bet. groups}}{\text{variability w/in groups}}$} ```{r, echo=F, message=F, warning=F,fig.width=5.5, fig.height=1.5,fig.align='center'} FTail <- function(U=NULL, df_n=100, df_d = 100, curveColor=1, border=1, col="#569BBD", xlim=NULL, ylim=NULL, xlab='', ylab='', detail=999){ if(U <= 5){xlim <- c(0,5)} if(U > 5){xlim <- c(0,U+0.01*U)} temp <- diff(range(xlim)) x <- seq(xlim[1] - temp/4, xlim[2] + temp/4, length.out=detail) y <- df(x, df_n, df_d) ylim <- range(c(0,y)) plot(x, y, type='l', xlim=xlim, ylim=ylim, axes=FALSE, col=curveColor, xlab = "", ylab = "",lwd=2) these <- (x >= U) X <- c(x[these][1], x[these], rev(x[these])[1]) Y <- c(0, y[these], 0) polygon(X, Y, border=border, col=col) abline(h=0) axis(1, at = c(0,U), label = c(NA,round(U,4))) } par(mar = c(0,0,0,0)) FTail(19,20,2, col = COL[1]) ``` - In order to be able to reject $H_0$, we need a small p-value, which requires a large F statistic. - In order to obtain a large F statistic, variability between sample means needs to be greater than variability within sample means. ## Degrees of freedom associated with ANOVA \begin{center} \begin{tabular}{llrrrrr} \hline & & Df & Sum Sq & Mean Sq & F value & Pr($>$F) \\ \hline (\alert{G}roup) & depth & 2 & 16.96 & 8.48 & 6.13 & 0.0063 \\ (\alert{E}rror) & Residuals & 27 & 37.33 & 1.38 & & \\ \hline & \alert{T}otal & 29 & 54.29 \\ \end{tabular} \end{center} \begin{itemize} \item groups: $df_G = k - 1$, where $k$ is the number of groups \item total: $df_T = n - 1$, where $n$ is the total sample size \item error: $df_E = df_T - df_G$ \end{itemize} \pause \begin{itemize} \item $df_G = k - 1 = 3 - 1 = 2$ \\ \pause \item $df_T = n - 1 = 30 - 1 = 29$ \pause \item $df_E = 29 - 2 = 27$ \\ \end{itemize} ## Sum of squares between groups, SSG \footnotesize \begin{center} \begin{tabular}{ll rrrrr} \hline & & Df & Sum Sq & Mean Sq & F value & Pr($>$F) \\ \hline (\alert{G}roup) & depth & 2 & \textcolor{red}{16.96} & 8.48 & 6.13 & 0.0063 \\ (\alert{E}rror) & Residuals & 27 & 37.33 & 1.38 & & \\ \hline & \alert{T}otal & 29 & 54.29 \\ \end{tabular} \end{center} \normalsize Measures the variability between groups \vspace{-0.25cm} \[ SSG = \sum_{i = 1}^{k} n_i (\bar{x}_i - \bar{x})^2 \] where $n_i$ is each group size, $\bar{x}_i$ is the average for each group, $\bar{x}$ is the overall (grand) mean. \pause \vspace{-0.5cm} \begin{columns} \begin{column}{0.4\textwidth} \small \begin{center} \begin{tabular}{l | c c } & n & mean \\ \hline bottom & 10 & 6.04 \\ middepth& 10 & 5.05 \\ surface & 10 & 4.2 \\ \hline overall & 30 & 5.1 \end{tabular} \end{center} \end{column} \pause \normalsize \begin{column}{0.5\textwidth} \begin{eqnarray*} SSG &=& \left( 10 \times (6.04 - 5.1)^2 \right) \\ \pause &+& \left( 10 \times (5.05 - 5.1)^2 \right) \\ \pause &+& \left( 10 \times (4.2 - 5.1)^2 \right) \\ \pause &=& 16.96 \\ \end{eqnarray*} \end{column} \end{columns} ## Sum of squares total, SST \begin{center} \begin{tabular}{ll rrrrr} \hline & & Df & Sum Sq & Mean Sq & F value & Pr($>$F) \\ \hline (\alert{G}roup) & depth & 2 & 16.96 & 8.48 & 6.13 & 0.0063 \\ (\alert{E}rror) & Residuals & 27 & 37.33 & 1.38 & & \\ \hline & \alert{T}otal & 29 & \textcolor{red}{54.29} \\ \end{tabular} \end{center} Measures the variability between groups \vspace{-0.25cm} \[ SST = \sum_{i = 1}^{n} (x_i - \bar{x})^2 \] where $x_i$ represent each observation in the dataset. \pause \vspace{-0.75cm} \begin{eqnarray*} SST &=& (3.8 - 5.1)^2 + (4.8 - 5.1)^2 + (4.9 - 5.1)^2 + \cdots + (5.2 - 5.1)^2 \\ \pause &=& (-1.3)^2 + (-0.3)^2 + (-0.2)^2 + \cdots + (0.1)^2 \\ \pause &=& 1.69 + 0.09 + 0.04 + \cdots + 0.01 \\ \pause &=& 54.29 \end{eqnarray*} ## Sum of squares error, SSE \begin{center} \begin{tabular}{ll rrrrr} \hline & & Df & Sum Sq & Mean Sq & F value & Pr($>$F) \\ \hline (\alert{G}roup) & depth & 2 & 16.96 & 8.48 & 6.13 & 0.0063 \\ (\alert{E}rror) & Residuals & 27 & \textcolor{red}{37.33} & 1.38 & & \\ \hline & \alert{T}otal & 29 & 54.29 \\ \end{tabular} \end{center} Measures the variability within groups: \[ SSE = SST - SSG \] \pause \[ SSE = 54.29 - 16.96 = 37.33 \] ## Mean square error \begin{center} \begin{tabular}{ll rrrrr} \hline & & Df & Sum Sq & Mean Sq & F value & Pr($>$F) \\ \hline (\alert{G}roup) & depth & 2 & 16.96 & \textcolor{red}{8.48} & 6.13 & 0.0063 \\ (\alert{E}rror) & Residuals & 27 & 37.33 & \textcolor{red}{1.38} & & \\ \hline & \alert{T}otal & 29 & 54.29 \\ \end{tabular} \end{center} Mean square error is calculated as sum of squares divided by the degrees of freedom. \pause \begin{eqnarray*} MSG &=& 16.96 / 2 = 8.48 \\ \pause MSE &=& 37.33 / 27 = 1.38 \end{eqnarray*} ## Test statistic, F value \begin{center} \begin{tabular}{ll rrrrr} \hline & & Df & Sum Sq & Mean Sq & F value & Pr($>$F) \\ \hline (\alert{G}roup) & depth & 2 & 16.96 & 8.48 & \textcolor{red}{6.14} & 0.0063 \\ (\alert{E}rror) & Residuals & 27 & 37.33 & 1.38 & & \\ \hline & \alert{T}otal & 29 & 54.29 \\ \end{tabular} \end{center} As we discussed before, the F statistic is the ratio of the between group and within group variability. \[ F = \frac{MSG}{MSE} \] \pause \[ F = \frac{8.48}{1.38} = 6.14 \] ## p-value \begin{center} \begin{tabular}{ll rrrrr} \hline & & Df & Sum Sq & Mean Sq & F value & Pr($>$F) \\ \hline (\alert{G}roup) & depth & 2 & 16.96 & 8.48 & \textcolor{red}{6.14} & 0.0063 \\ (\alert{E}rror) & Residuals & 27 & 37.33 & 1.38 & & \\ \hline & \alert{T}otal & 29 & 54.29 \\ \end{tabular} \end{center} p-value is the probability of at least as large a ratio between the ``between group" and ``within group" variability, if in fact the means of all groups are equal. It's calculated as the area under the F curve, with degrees of freedom $df_G$ and $df_E$, above the observed F statistic. \pause {height="45%"} ## Conclusion - in context \alert{What is the conclusion of the hypothesis test?} The data provide convincing evidence that the average aldrin concentration A) is different for all groups. B) on the surface is lower than the other levels. C) is different for at least one group. D) is the same for all groups. ## Conclusion - in context \alert{What is the conclusion of the hypothesis test?} The data provide convincing evidence that the average aldrin concentration A) is different for all groups. B) on the surface is lower than the other levels. C) \alert{is different for at least one group.} D) is the same for all groups. ## Conclusion - If p-value is small (less than $\alpha$), reject $H_0$. The data provide convincing evidence that at least one mean is different from (but we can't tell which one). \pause - If p-value is large, fail to reject $H_0$. The data do not provide convincing evidence that at least one pair of means are different from each other, the observed differences in sample means are attributable to sampling variability (or chance). ## Independence \alert{Does this condition appear to be satisfied?} \pause In this study, we have no reason to believe that the aldrin concentration won't be independent of each other. ## Approximately normal \alert{Does this condition appear to be satisfied?} ```{r, echo=F, message=F, warning=F,out.width="75%",fig.align='center'} par(mar=c(2,4,2,1), las=1, mgp=c(3,0.7,0), cex.lab = 1.25, cex.axis = 1.25, mfrow = c(1,3)) hist(aldrin$aldrin[aldrin$depth == "bottom"], col = COL[1], main = "", ylab = "", axes = FALSE, cex.axis = 2) axis(1, at = c(3,5,7,9)) axis(2, at = c(0,1,2,3)) hist(aldrin$aldrin[aldrin$depth == "middepth"], col = COL[1], main = "", ylab = "", axes = FALSE, cex.axis = 2) axis(1, at = c(3,5,7)) axis(2, at = c(0,1,2)) hist(aldrin$aldrin[aldrin$depth == "surface"], col = COL[1], main = "", ylab = "", axes = FALSE, xlim = c(2.5,5.5), cex.axis = 2) axis(1, at = c(2.5,4,5.5)) axis(2, at = c(0,1,2,3,4)) ``` ## Constant variance \alert{Does this condition appear to be satisfied?} ```{r, echo=F, message=F, warning=F,out.width="75%",fig.align='center'} par(mar=c(3,3,2,1), las=1, mgp=c(3,1.9,0), cex.lab = 1.25, cex.axis = 2, mfrow = c(1,1)) boxplot(aldrin$aldrin ~ aldrin$depth, names = c("bottom\nsd=1.58","middepth\nsd=1.10","surface\nsd=0.66")) ``` ## Which means differ? - Earlier we concluded that at least one pair of means differ. The natural question that follows is "which ones?" \pause - We can do two sample $t$ tests for differences in each possible pair of groups. \pause \alert{Can you see any pitfalls with this approach?} \pause - When we run too many tests, the Type 1 Error rate increases. - This issue is resolved by using a modified significance level. ## Multiple comparisons - The scenario of testing many pairs of groups is called **multiple comparisons**. \pause - The **Bonferroni correction** suggests that a more \alert{stringent} significance level is more appropriate for these tests: \centering{$\alpha^* = \alpha / K$} \raggedright where $K$ is the number of comparisons being considered. \pause - If there are $k$ groups, then usually all possible pairs are compared and $K = \frac{k(k-1)}{2}$ ## Determining the modified $\alpha$ \alert{In the aldrin data set depth has 3 levels: bottom, mid-depth, and surface. If $\alpha = 0.05$, what should be the modified significance level for two sample $t$ tests for determining which pairs of groups have significantly different means?} A) $\alpha^* = 0.05$ B) $\alpha^* = 0.05/2 = 0.025$ C) $\alpha^* = 0.05/3 = 0.0167$ D) $\alpha^* = 0.05/6 = 0.0083$ ## Determining the modified $\alpha$ \alert{In the aldrin data set depth has 3 levels: bottom, mid-depth, and surface. If $\alpha = 0.05$, what should be the modified significance level for two sample $t$ tests for determining which pairs of groups have significantly different means?} A) $\alpha^* = 0.05$ B) $\alpha^* = 0.05/2 = 0.025$ C) \textcolor{red}{$\alpha^* = 0.05/3 = 0.0167$} D) $\alpha^* = 0.05/6 = 0.0083$ ## Which means differ? \alert{Based on the box plots below, which means would you expect to be significantly different?} \begin{columns} \begin{column}{0.6\textwidth} ```{r, echo=F, message=F, warning=F,out.width="100%",fig.align='center'} par(mar=c(3,3,2,1), las=1, mgp=c(3,1.9,0), cex.lab = 1.25, cex.axis = 1.5, mfrow = c(1,1)) boxplot(aldrin$aldrin ~ aldrin$depth, names = c("bottom\nsd=1.58","middepth\nsd=1.10","surface\nsd=0.66")) ``` \end{column} \begin{column}{0.35\textwidth} \small A) bottom \& surface B) bottom \& mid-depth C) mid-depth \& surface D) bottom \& mid-depth; \\ mid-depth \& surface E) bottom \& mid-depth; \\ bottom \& surface; \\ mid-depth \& surface \end{column} \end{columns} ## Which means differ? If the ANOVA assumption of equal variability across groups is satisfied, we can use the data from all groups to estimate variability: - Estimate any within-group standard deviation with $\sqrt{MSE}$, which is $s_{pooled}$. - Use the error degrees of freedom, $n-k$, for $t$-distributions. **Difference in two means: after ANOVA** \centering{$SE = \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}} \approx \sqrt{\frac{MSE}{n_1}+\frac{MSE}{n_2}}$} ## \alert{Is there a difference between the average aldrin concentration at the bottom and at mid depth?} \begin{columns} \begin{column}{0.4\textwidth} \scriptsize \begin{center} \begin{tabular}{l | c c c} & n & mean & sd \\ \hline bottom & 10 & \alert{6.04} & 1.58 \\ middepth& 10 & \alert{5.05} & 1.10 \\ surface & 10 & 4.2 & 0.66 \\ \hline overall & 30 & 5.1 & 1.37 \end{tabular} \end{center} \end{column} \begin{column}{0.7\textwidth} \scriptsize \begin{center} \begin{tabular}{l rrrrr} \hline & Df & Sum Sq & Mean Sq & F value & Pr($>$F) \\ \hline depth & 2 & 16.96 & 8.48 & 6.13 & 0.0063 \\ Residuals & \alert{27} & 37.33 & \alert{1.38} & & \\ \hline Total & 29 & 54.29 \\ \end{tabular} \end{center} \end{column} \end{columns} \begin{eqnarray*} T_{df_E} &=& \frac{(\bar{x}_{bottom} - \bar{x}_{middepth})}{\sqrt{ \frac{MSE}{n_{bottom}} + \frac{MSE}{n_{middepth}} }} \\ \pause T_{27} &=& \frac{( 6.04 - 5.05 )}{\sqrt{ \frac{1.38}{10} + \frac{1.38}{10} }} = \frac{0.99}{0.53} =1.87 \\ \pause 0.05 &<& p-value < 0.10 \qquad \text \\ \pause \alpha^\star &=& 0.05 / 3 = 0.0167 \end{eqnarray*} \pause \small Fail to reject $H_0$, data do not provide convincing evidence of a difference between average aldrin concentrations at bottom and mid depth. ## Pairwise comparisons \alert{Is there a difference between the average aldrin concentration at the bottom and at surface?} \pause \begin{eqnarray*} T_{df_E} &=& \frac{(\bar{x}_{bottom} - \bar{x}_{surface})}{\sqrt{ \frac{MSE}{n_{bottom}} + \frac{MSE}{n_{surface}} }} \\ \pause T_{27} &=& \frac{( 6.04 - 4.2 )}{\sqrt{ \frac{1.38}{10} + \frac{1.38}{10} }} = \frac{1.84}{0.53} =3.47 \\ \pause p-value = 0.0018 \qquad \text{\footnotesize (two-sided)} \\ \pause \alpha^\star &=& 0.05 / 3 = 0.0167 \end{eqnarray*} \pause \small Reject $H_0$, the data provide convincing evidence of a difference between the average aldrin concentrations at bottom and surface.