```{r setup, include=FALSE} knitr::opts_chunk$set(echo = FALSE) ``` ```{r, echo=F, message=F, warning=F} library(readr) library(openintro) library(here) library(tidyverse) data(COL) ``` # Point estimates and sampling variability ## Point estimates and error - We are often interested in **population parameters**. - Complete populations are difficult to collect data on, so we use **sample statistics** as **point estimates** for the unknown population parameters of interest. - **Error** in the estimate $\rightarrow$ difference between population parameter and sample statistic. - Generally, the **error** in the estimate consists of two aspects: - **Bias** is systematic tendency to over- or under-estimate the true population parameter. - **Sampling error** describes how much an estimate will tend to vary from one sample to the next. - Much of statistics is focused on understanding and quantifying sampling error, and **sample size** is helpful for quantifying this error. ## Practice \alert{Suppose we randomly sample 1,000 adults from each state in the U.S. Would you expect the sample means of their heights to be the same, somewhat different, or very different?} \pause Not the same, but only somewhat different. ##   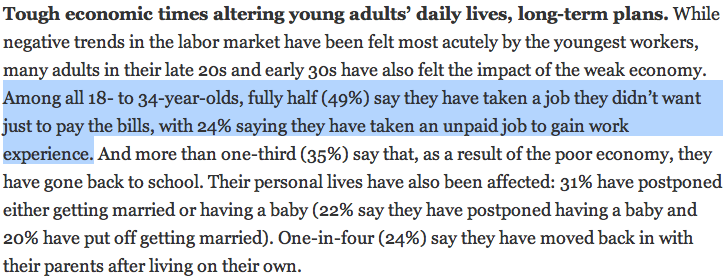 ## Margin of error  - $41\% \pm 2.9\%:$ We are 95% confident that 38.1% to 43.9% of the public believe young adults, rather than middle-aged or older adults, are having the toughest time in today's economy. - $49\% \pm 4.4\%:$ We are 95% confident that 44.6% to 53.4% of 18-34 years old have taken a job they didn't want just to pay the bills. ## Practice \alert{Suppose the proportion of American adults who support the expansion of solar energy is p = 0.88, which is our parameter of interest. Is a randomly selected American adult more or less likely to supoort the expansion of solar energy?} \pause More likely. ## \alert{Suppose that you don't have access to the population of all American adults, which is a quite likely scenario. In order to estimate the proportion of American adults who support solar power expansion, you might sample from the population and use your sample proportion as the best guess for the unknown population proportion.} - Sample, without replacement, 1000 American adults from the population, and record whether they support or not solar power expansion. - Find the sample proportion. - Plot the distribution of the sample proportions obtained by members of the class. ## ```{r, echo=T} # 1. Create a set of 330 million entries, where 88% # of them are "support" and 12% are "not". pop_size <- 330000000 possible_entries <- c(rep("support", 0.88 * pop_size), rep("not", 0.12 * pop_size)) # 2. Sample 1000 entries without replacement. sampled_entries <- sample(possible_entries, size = 1000, replace = F) # 3. Compute p-hat: count the number that are # "support", then divide by # of the sample size sum(sampled_entries == "support")/1000 ``` ## Sampling distribution Suppose you were to repeat this process many times and obtain many $\hat{p}$s. This distribution is called a sampling distribution. ```{r, echo=F, message=F, warning=F, fig.width=8, fig.height=4,fig.align='center'} phat <- rep(NA, 10000) for(i in 1:10000){ sampled_entries <- sample(possible_entries, size = 1000) phat[i] <- sum(sampled_entries == "support") / 1000 } # df sampling <- tibble(phat = phat) # plot ggplot(sampling, aes(x = phat)) + geom_histogram(binwidth = 0.01, fill = COL[1]) + theme_minimal(base_size = 14) + labs(x = "Simulated sample proportion", y = "") ``` ## Practice \alert{What is the shape and center of this distribution? Based on this distribution, what do you think is the true population proportion?} ```{r, echo=F, message=F, warning=F, fig.width=8, fig.height=4,fig.align='center'} ggplot(sampling, aes(x = phat)) + geom_histogram(binwidth = 0.01, fill = COL[1]) + theme_minimal(base_size = 14) + labs(x = "Simulated sample proportion", y = "") ``` \pause The distribution is unimodal and roughly symmetric. A reasonable guess for the true population proportion is the center of this distribution, approximately 0.88. ## Sampling distributions are never observed - In real-world applications, we never actually observe the sampling distribution, yet it is useful to always think of a point estimate as coming from such a hypothetical distribution. - Understanding the sampling distribution will help us characterize and make sense of the point estimates that we do observe. ## Central Limit Theorem Sample proportions will be nearly normally distributed with mean equal to the population proportion, $p$, and standard error equal to $\sqrt{\frac{p(1-p)}{n}}$. \centering{$\hat{p} \sim N \left(mean=p, SE = \sqrt{\frac{p(1-p)}{n}} \right)$} - It wasn't a coincidence that the sampling distribution we saw earlier was symmetric, and centered at the true population proportion. - We won't go through a detailed proof of why $SE = \sqrt{\frac{p(1-p)}{n}}$, but note that as $n$ increases $SE$ decreases. - As $n$ increases samples will yield more consistent $\hat{p}$s, i.e. variability among $\hat{p}$s will be lower. ## CLT - conditions Certain conditions must be met for the CLT to apply: \begin{enumerate} \item \textbf{Independence:} Sampled observations must be independent. This is difficult to verify, but is more likely if \begin{itemize} \small \item random sampling/assignment is used, and \item if sampling without replacement, $n < 10\%$ of the population. \normalsize \end{itemize} \item \textbf{Sample size:} There should be at least 10 expected successes and 10 expected failures in the observed sample. This is difficult to verify if you don't know the population proportion (or can't assume a value for it). In those cases we look for the number of observed successes and failures to be at least 10. \end{enumerate} ## When $p$ is unknown - The CLT states $SE = \sqrt{\frac{p(1-p)}{n}}$, with the condition that $np$ and $n(1-p)$ are at least 10, however we often don't know the value of $p$, the population proportion. - In these cases we substitute $\hat{p}$ for $p$. ## When $p$ is low \alert{Suppose we have a population where the true population proportion is $p=0.05,$ and we take random sample of size $n = 50$ from this population. We calculate the sample proportion in each sample and plot these proportions. Would you expect this distribution to be nearly normal? Why, or why not?} \pause No, the success-failure condition is not met $(50 *0.05 = 2.5)$, hence we would not expect the sampling distribution to be nearly normal. ```{r, echo=F, message=F, warning=F, fig.width=4, fig.height=1.8,fig.align='center'} p <- 0.05 N <- 100000000 ones <- N * p zeros <- N * (1-p) pop <- c(rep(1, ones), rep(0, zeros)) n <- 50 set.seed(12345) sampling <- tibble( phat = rep(NA, 1000) ) for(i in 1:nrow(sampling)){ sampling$phat[i] <- sum(sample(pop, n)) / n } ggplot(sampling, aes(x = phat)) + geom_histogram(binwidth = 0.01, fill = COL[1]) + theme_minimal() + labs(x = "Simulated sample proportion", y = "") ``` ## \alert{What happens when $np$ and/or $n(1-p)<10$?} \begin{multicols}{2} \includegraphics[width=1\columnwidth]{clt_prop_grid_1.pdf} \columnbreak \includegraphics[width=1\columnwidth]{clt_prop_grid_2.pdf} \end{multicols} ## When the conditions are not met... - When either $np$ or $n(1-p)$ is small, the distribution is more discrete. - When $np$ or $n(1-p)<10$, the distribution is more skewed. - The larger both $np$ and $n(1-p)$, the more normal the distribution. - When $np$ and $n(1-p)$ are both very large, the discreteness of the distribution is hardly evident, and the distribution looks much more like a normal distribution. ## Extending the framework for other statistics - The strategy of using sample statistic to estimate a parameter is quite common, and it's a strategy that we can apply to other statistics besides a proportion. - Take a random sample of students at a college and ask them how many extracurricular activities they are involved in to estimate the average number of extra curricular activities all students in this college are interested in. - The principles and general ideas are from this chapter apply to other parameters as well, even if the details change a little.