```{r setup, include=FALSE} knitr::opts_chunk$set(echo = FALSE) ``` ```{r, echo=F, message=F, warning=F} library(readr) library(openintro) data(COL) ``` # Normal distibution ## Normal distribution - Unimodal and symmetric, bell shaped curve. - Many variables are nearly normal, but none are exactly normal. - Denoted as $\textcolor{red}{N(\mu, \sigma)}$ $\rightarrow$ Normal with mean $\mu$ and standard deviation $\sigma$. ```{r, echo=F, message=F, warning=F, fig.width=4, fig.height=2,fig.align='center'} #===> plot <===# par(mfrow=c(1,1), las=1, mar=0.5*c(1,1,1,1)) # curve 1 X <- seq(-4,4,0.01) Y <- dnorm(X) plot(X, Y, type='l', axes=F, xlim=c(-3.4,3.4), col='#335588', lwd=4) #axis(1, at=-3:3) abline(h=-0.002, col='#888888') ``` ## Heights of males \begin{multicols}{2} \includegraphics[width=1\columnwidth]{ok_cupid_men.png} \columnbreak \pause "The male heights on OkCupid very nearly follow the expected normal distribution \- except the whole thing is shifted to be right of where it should be. Almost universally guys like to add a couple inches." "You can also see a more subtle vanity at work: starting at roughly 5'8", the top of the dotted curve tilts even further rightward. This means that guys as they get closer to six feet round up a bit more than usual, stretching for that coveted psychological benchmark." \end{multicols} ## Heights of females \begin{multicols}{2} \includegraphics[width=1\columnwidth]{ok_cupid_women.png} \columnbreak \pause "When we looked into the data for women, we were surprised to see height exaggeration was just as widespread, though without the lurch towards a benchmark height." \end{multicols} ## Normal distributions with different parameters \centering{$\mu:$ mean, $\sigma:$ standard deviation} ```{r, echo=F, message=F, warning=F, fig.width=4, fig.height=2,fig.align='center',include=F} set.seed(1) x <- rnorm(100000) hold <- hist(x, breaks=50, prob=T) ``` ```{r, echo=F, message=F, warning=F, fig.width=3, fig.height=1.5,fig.align='center'} #===> plot <===# par(mfrow=c(1,2), las=1, mar=c(2.5,1,0.5,1)) #main = bquote('N('~mu==.0~','~sigma==.1~')') # curve 1 X <- seq(-4,4,0.01) Y <- dnorm(X) plot(X, Y, type='l', axes=F, xlim=c(-3.4,3.4), main = bquote('N('~mu==.0~','~sigma==.1~')'),line=-0.01) axis(1, at=-3:3) for(i in 1:length(hold$counts)){ rect(hold$breaks[i], 0, hold$breaks[i+1], hold$density[i], border='#DDDDDD', col='#F4F4F4') } lines(X, Y) abline(h=0) # curve 2 X <- seq(3,35,0.01) Y <- dnorm(X, 19, 4) plot(X, Y, type='l', axes=F, xlim=c(5.4,32.6), main = bquote('N('~mu==.19~','~sigma==.4~')'),line=-0.01) axis(1, at=19+4*(-3:3)) for(i in 1:length(hold$counts)){ rect(19+4*hold$breaks[i], 0, 19+4*hold$breaks[i+1], hold$density[i]/4, border='#DDDDDD', col='#F4F4F4') } lines(X, Y) abline(h=0) ``` ```{r, echo=F, message=F, warning=F, fig.width=4, fig.height=2,fig.align='center',include=F} set.seed(1) x <- rnorm(100000) hold <- hist(x, breaks=50, prob=T) ``` ```{r, echo=F, message=F, warning=F, fig.width=3, fig.height=1.5,fig.align='center'} #===> plot <===# par(mfrow=c(1,1), las=1, mar=c(2.5,1,0.5,1)) # curve 1 X <- seq(-4,4,0.01) Y <- dnorm(X) plot(X, Y, type='l', axes=F, xlim=c(-5,35)) axis(1, at=seq(-10, 40, 10)) lines(X, Y) abline(h=0) # curve 2 X <- seq(3,35,0.01) Y <- dnorm(X, 19, 4) lines(X, Y) ``` ## Practice \alert{SAT scores are distributed nearly normally with mean 1500 and standard deviattion 300. ACT scores are distributed nearly normally with mean 21 and statdard deviation 5. A college admissions officer wants to determine which of the two applicants scored better on their standardized test with respect to the other test takers: Pam, who earned an 1800 on her SAT, or Jim, who scored a 24 on his ACT?} ```{r, echo=F, message=F, warning=F, fig.width=4, fig.height=1.8,fig.align='center'} par(mfrow=c(1,2), mar=c(2.1,0,0,0), cex = 1.25) m = 1500 s = 300 normTail(m = 1500, s = 300) lines(c(m,m), dnorm(m, m, s)*c(0.01,0.99), lty=2, col='#EEEEEE') lines(c(m,m)+s, dnorm(m+s, m, s)*c(0.01,1.25), lty=2, col='#335588') text(m+s, dnorm(m+s,m,s)*1.25, 'Pam', pos=4, col='#335588', cex = 0.7) m = 21 s = 5 normTail(m = 21, s = 5) lines(c(m,m), dnorm(m, m, s)*c(0.01,0.99), lty=2, col='#EEEEEE') lines(c(24,24), dnorm(m+3, m, s)*c(0.01,1.04), lty=2, col="red") text(24, dnorm(24,m,s)*1.05, 'Jim', pos=4, col="red", cex = 0.7) ``` ## Standardizing with Z scores Since we cannot just compare these two raw scores, we instead compare how many standard deviations beyond the mean each observation is: - Pam's score is $\frac{1800-1500}{300} = 1$ standard deviation above the mean. - Jim's score is $\frac{24-21}{5} = 0.6$ standard deviations above the mean. ```{r, echo=F, message=F, warning=F, fig.width=4, fig.height=1.8,fig.align='center'} par(mfrow=c(1,1), las=1, mar=c(2,0.5,0,0.5)) m <- 0 s <- 1 X <- m+s*seq(-4,4,0.01) Y <- dnorm(X, m, s) plot(X, Y, type='l', axes=F, xlim=m+s*c(-2.7,2.7)) axis(1, at=m+s*(-3:3)) abline(h=0) lines(c(m,m), dnorm(m, m, s)*c(0.01,0.99), lty=2, col='#EEEEEE') lines(c(m,m)+s, dnorm(m+s, m, s)*c(0.01,1.5), lty=2, col='#335588') lines(c(m,m)+0.6*s, dnorm(m+0.6*s, m, s)*c(0.01,1.1), lty=2, col="red") text(m+s, dnorm(m+s,m,s)*1.5, ' Pam', pos=4, col='#335588') text(m+0.6*s, dnorm(m+0.6*s,m,s)*1.1, 'Jim', pos=4.6, col="red") ``` ## Standardizing with Z scores - These are called **standardized** scores, or **Z scores**. - Z score of an observation is the number of standard deviations it falls above or below the mean. \centering{$Z = \frac{observation - mean}{SD}$} - Z scores are define for distributions of any shape, but only when the distribution is normal can we use Z scores to calculate percentiles. - Observations that are more than 2 SD away from the mean ($|Z| > 2$) are usually considered unusual. ## Percentiles - **Percentile** is the percentage of observations that fall below a given data point. - Graphically, percentile is the are below the probability distribution curve to the left of that observation. ```{r, echo=F, message=F, warning=F, fig.width=4, fig.height=1.8,fig.align='center'} #===> plot <===# par(las=1, mar=c(1.5,0,0.5,0), mgp=c(3,0.6,0)) X <- seq(-4,4,0.01) Y <- dnorm(X) plot(X, Y, type='l', axes=F, xlim=c(-3.4,3.4)) axis(1, at=-3:3, label=(1500+300*(-3:3)), cex.axis=0.7) these <- which(X <= 1) polygon(c(X[these[1]], X[these],X[rev(these)[1]]), c(0,Y[these],0), col='#CCCCCC') #arrows(1.3,0.28, 0.43, 0.28, length=0.07) #text(1.3, 0.28, 'X=1630\nZ=0.43', pos=4, cex=0.7) lines(X, Y) abline(h=0) ``` ## Calculating percentiles - using computation The are many ways to compute percentiles/areas under the curve: - **Applet:** [https://gallery.shinyapps.io/dist_calc/](https://gallery.shinyapps.io/dist_calc/) 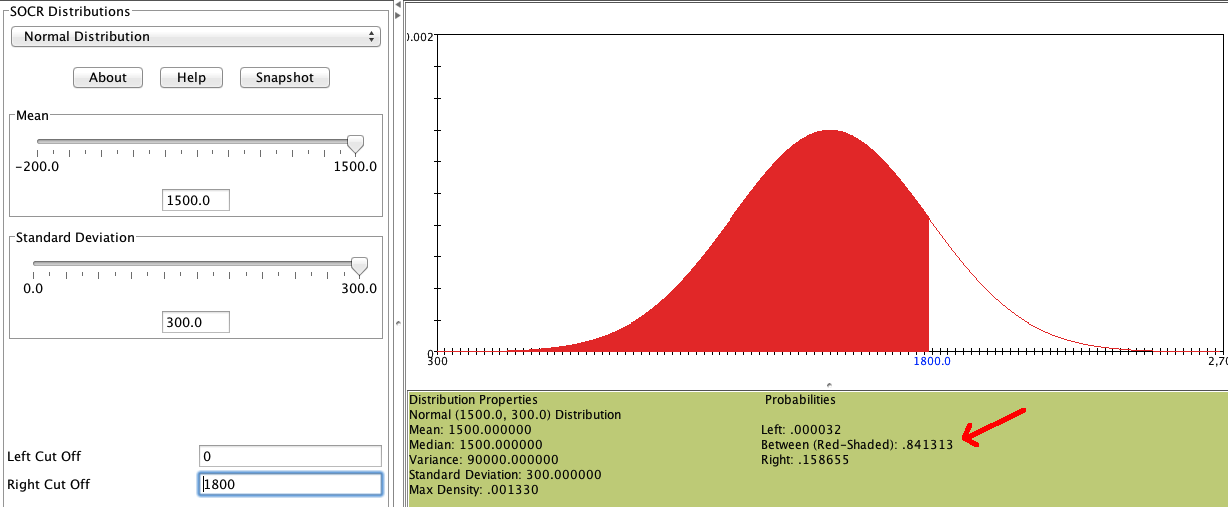 ## Calculating percentiles - using tables \footnotesize \begin{tabular}{c | rrrrr | rrrrr |} \cline{2-11} &&&& \multicolumn{4}{c}{Second decimal place of $Z$} &&& \\ \cline{2-11} $Z$ & 0.00 & 0.01 & 0.02 & 0.03 & 0.04 & 0.05 & 0.06 & 0.07 & 0.08 & 0.09 \\ \hline \hline 0.0 & \tiny{0.5000} & \tiny{0.5040} & \tiny{0.5080} & \tiny{0.5120} & \tiny{0.5160} & \tiny{0.5199} & \tiny{0.5239} & \tiny{0.5279} & \tiny{0.5319} & \tiny{0.5359} \\ 0.1 & \tiny{0.5398} & \tiny{0.5438} & \tiny{0.5478} & \tiny{0.5517} & \tiny{0.5557} & \tiny{0.5596} & \tiny{0.5636} & \tiny{0.5675} & \tiny{0.5714} & \tiny{0.5753} \\ 0.2 & \tiny{0.5793} & \tiny{0.5832} & \tiny{0.5871} & \tiny{0.5910} & \tiny{0.5948} & \tiny{0.5987} & \tiny{0.6026} & \tiny{0.6064} & \tiny{0.6103} & \tiny{0.6141} \\ 0.3 & \tiny{0.6179} & \tiny{0.6217} & \tiny{0.6255} & \tiny{0.6293} & \tiny{0.6331} & \tiny{0.6368} & \tiny{0.6406} & \tiny{0.6443} & \tiny{0.6480} & \tiny{0.6517} \\ 0.4 & \tiny{0.6554} & \tiny{0.6591} & \tiny{0.6628} & \tiny{0.6664} & \tiny{0.6700} & \tiny{0.6736} & \tiny{0.6772} & \tiny{0.6808} & \tiny{0.6844} & \tiny{0.6879} \\ \hline 0.5 & \tiny{0.6915} & \tiny{0.6950} & \tiny{0.6985} & \tiny{0.7019} & \tiny{0.7054} & \tiny{0.7088} & \tiny{0.7123} & \tiny{0.7157} & \tiny{0.7190} & \tiny{0.7224} \\ 0.6 & \tiny{0.7257} & \tiny{0.7291} & \tiny{0.7324} & \tiny{0.7357} & \tiny{0.7389} & \tiny{0.7422} & \tiny{0.7454} & \tiny{0.7486} & \tiny{0.7517} & \tiny{0.7549} \\ 0.7 & \tiny{0.7580} & \tiny{0.7611} & \tiny{0.7642} & \tiny{0.7673} & \tiny{0.7704} & \tiny{0.7734} & \tiny{0.7764} & \tiny{0.7794} & \tiny{0.7823} & \tiny{0.7852} \\ 0.8 & \tiny{0.7881} & \tiny{0.7910} & \tiny{0.7939} & \tiny{0.7967} & \tiny{0.7995} & \tiny{0.8023} & \tiny{0.8051} & \tiny{0.8078} & \tiny{0.8106} & \tiny{0.8133} \\ 0.9 & \tiny{0.8159} & \tiny{0.8186} & \tiny{0.8212} & \tiny{0.8238} & \tiny{0.8264} & \tiny{0.8289} & \tiny{0.8315} & \tiny{0.8340} & \tiny{0.8365} & \tiny{0.8389} \\ \hline \hline 1.0 & \textcolor{red}{\tiny{0.8413}} & \tiny{0.8438} & \tiny{0.8461} & \tiny{0.8485} & \tiny{0.8508} & \tiny{0.8531} & \tiny{0.8554} & \tiny{0.8577} & \tiny{0.8599} & \tiny{0.8621} \\ 1.1 & \tiny{0.8643} & \tiny{0.8665} & \tiny{0.8686} & \tiny{0.8708} & \tiny{0.8729} & \tiny{0.8749} & \tiny{0.8770} & \tiny{0.8790} & \tiny{0.8810} & \tiny{0.8830} \\ 1.2 & \tiny{0.8849} & \tiny{0.8869} & \tiny{0.8888} & \tiny{0.8907} & \tiny{0.8925} & \tiny{0.8944} & \tiny{0.8962} & \tiny{0.8980} & \tiny{0.8997} & \tiny{0.9015} \\ \end{tabular} ## Six Sigma "The term six sigma process comes from the notion that if one has six standard deviations between the process mean and the nearest specification limit, as shown in the graph, practically no items will fail to meet specifications." \centering {width="60%"} ## Quality control \alert{At Heinz ketchup factory the amounts which go into bottles of ketchup are supposed to be normally distributed with mean 36 oz. and standard deviation 0.11 oz. Once every 30 minutes a bottle is selected from the production line, and is below 35.8 oz. or above 36.2 oz., then the bottle fails the quality control inspection. What percent of bottles have less than 35.8 ounces of ketchup?} \pause Let $X =$ amount of ketchup in a bottle: $X \sim N(\mu = 36, \sigma = 0.11)$ \pause \begin{multicols}{2} ```{r, echo=F, message=F, warning=F, fig.width=4, fig.height=1.8,fig.align='center'} par(mar=c(2.1,0,0,0)) normTail(m = 36, s = 0.11, L = 35.8, axes = FALSE, col = COL[1], lwd = 2) axis(1, at=c(35.67, 35.8, 36, 36.33), label=expression("", "35.8", "36", "")) ``` \columnbreak \pause $Z = \frac{35.8-36}{0.11}=-1.82$ \end{multicols} ## Practice \alert{What percent of bottles \underline{pass} the quality control inspection?} A) 1.82% B) 3.44% C) 6.88% D) 93.12% E) 96.56% ## Practice \alert{What percent of bottles \underline{pass} the quality control inspection?} A) 1.82% B) 3.44% C) 6.88% D) \alert{93.12\%} E) 96.56% \pause \begin{multicols}{3} ```{r, echo=F, message=F, warning=F, fig.width=5, fig.height=2,fig.align='center'} par(mar=c(2.1,0,0,0)) normTail(m = 36, s = 0.11, M = c(35.8, 36.2), axes = FALSE, col = COL[1], main = "=", line=-4, adj = 1) axis(1, at=c(35.67, 35.8, 36, 36.2, 36.33), label=expression("", "35.8", "36", "36.2", "")) ``` \columnbreak \pause ```{r, echo=F, message=F, warning=F, fig.width=5, fig.height=2,fig.align='center'} par(mar=c(2.1,0,0,0)) normTail(m = 36, s = 0.11, L = 36.2, axes = FALSE, col = COL[1], main = "-", line=-4, adj = 1) axis(1, at=c(35.67, 36, 36.2, 36.33), label=expression("", "36", "36.2", "")) ``` \columnbreak ```{r, echo=F, message=F, warning=F, fig.width=5, fig.height=2,fig.align='center'} par(mar=c(2.1,0,0,0)) normTail(m = 36, s = 0.11, L = 35.8, axes = FALSE, col = COL[1]) axis(1, at=c(35.67, 35.8, 36, 36.33), label=expression("", "35.8", "36", "")) ``` \end{multicols} \pause \centering{$Z_{35.8} = \frac{35.8-36}{0.11}=-1.82$} \pause \centering{$Z_{36.2} = \frac{36.2-36}{0.11}=1.82$} \pause \begin{align*} P(35.8x)=0.10$ \\ $P(Z<\textcolor{red}{1.28}) = 0.90$} \footnotesize\centering{$Z = \frac{obs-mean}{SD} \rightarrow \frac{x-98.2}{0.73} = 1.28$} \footnotesize\centering{$x = (1.28 \times 0.73)+98.2=99.1$} \end{multicols} ## 68 - 95 - 99.7 Rule - For nearly normally distributed data, - about 68\% falls within 1 SD of the mean, - about 95\% falls within 2 SD of the mean, - about 99.7\% falls within 3 SD of the mean. - It is possible for observations to fall 4, 5, or more standard deviations away from the mean, but these occurrences are very rare if the data are nearly normal. ```{r, echo=F, message=F, warning=F, fig.width=6, fig.height=2.5,fig.align='center'} #===> plot <===# par(las=1, mar=c(2.5,0,0.3,0)) X <- seq(-4,4,0.01) Y <- dnorm(X) plot(X, Y, type='n', axes=F, ylim=c(0,0.4), xlim=c(-3.2,3.2)) abline(h=0, col='#AAAAAA') axis(1, at=-3:3, label=expression(mu-3*sigma,mu-2*sigma,mu-sigma,mu, mu+sigma,mu+2*sigma,mu+3*sigma)) COL <- c('#DFF0E8', '#CFC8D8', '#B8AFA8') for(i in 3:1){ these <- (X>=-i & X <= i) polygon(c(-i,X[these],i),c(0,Y[these],0), col=COL[i], border=COL[i]) } #lines(c(0,0),c(0,dnorm(0)), col='#888888') #===> label 99.7 <===# arrows(-3,0.03, 3,0.03, code=3, col='#666666', length=0.15) #lines(c(-3,-3), c(0,0.03), lty=3, col='#888888') #lines(c(3,3), c(0,0.03), lty=3, col='#888888') text(0, 0.02, '99.7%', col='#333333', pos=3) #===> label 95 <===# arrows(-2,0.13, 2,0.13, code=3, col='#666666', length=0.15) #lines(c(-2,-2), c(0,0.13), lty=3, col='#888888') #lines(c(2,2), c(0,0.13), lty=3, col='#888888') text(0, 0.12, '95%', col='#333333', pos=3) #===> label 68 <===# arrows(-1,0.23, 1,0.23, code=3, col='#666666', length=0.15) #lines(c(-1,-1), c(0,0.23), lty=3, col='#888888') #lines(c(1,1), c(0,0.23), lty=3, col='#888888') text(0, 0.22, '68%', col='#333333', pos=3) lines(X, Y, col='#888888') abline(h=0, col='#AAAAAA') ``` ## Describing variability using the 68 - 95 - 99.7 Rule SAT scores are distributed nearly normally with mean 1500 and standard deviation 300. \pause - $\sim$ 68\% of students score between 1200 and 1800 on the SAT. - $\sim$ 95\% of students score between 900 and 2100 on the SAT. - $\sim$ 99.7\% of students score between 600 and 2400 on the SAT. ```{r, echo=F, message=F, warning=F, fig.width=6, fig.height=2.5,fig.align='center'} #===> plot <===# par(las=1, mar=c(2.5,0,0.3,0)) X <- seq(-4,4,0.01) Y <- dnorm(X) plot(X, Y, type='n', axes=F, ylim=c(0,0.4), xlim=c(-3.2,3.2)) abline(h=0, col='#AAAAAA') axis(1, at=-3:3, label=c("600","900","1200","1500","1800","2100","2400")) COL <- c('#DFF0E8', '#CFC8D8', '#B8AFA8') for(i in 3:1){ these <- (X>=-i & X <= i) polygon(c(-i,X[these],i),c(0,Y[these],0), col=COL[i], border=COL[i]) } #lines(c(0,0),c(0,dnorm(0)), col='#888888') #===> label 99.7 <===# arrows(-3,0.03, 3,0.03, code=3, col='#666666', length=0.15) #lines(c(-3,-3), c(0,0.03), lty=3, col='#888888') #lines(c(3,3), c(0,0.03), lty=3, col='#888888') text(0, 0.02, '99.7%', col='#333333', pos=3) #===> label 95 <===# arrows(-2,0.13, 2,0.13, code=3, col='#666666', length=0.15) #lines(c(-2,-2), c(0,0.13), lty=3, col='#888888') #lines(c(2,2), c(0,0.13), lty=3, col='#888888') text(0, 0.12, '95%', col='#333333', pos=3) #===> label 68 <===# arrows(-1,0.23, 1,0.23, code=3, col='#666666', length=0.15) #lines(c(-1,-1), c(0,0.23), lty=3, col='#888888') #lines(c(1,1), c(0,0.23), lty=3, col='#888888') text(0, 0.22, '68%', col='#333333', pos=3) lines(X, Y, col='#888888') abline(h=0, col='#AAAAAA') ``` ## Numer of hours of sleep on school nights ```{r, echo=F, message=F, warning=F, fig.width=6, fig.height=3,fig.align='center'} d = read.csv("dataset/sleep.csv") sleep = d$sleep[!is.na(d$sleep)] n = length(sleep) m = mean(sleep) s = sd(sleep) data(COL) # sleep-hist par(mar = c(2.5,2.5,0,0), las = 1) hist(sleep, col = COL[1], main = "", xlab = "", ylab = "", axes = FALSE) axis(1, cex.axis = 1.5) axis(2, at = seq(0,80,20), cex.axis = 1.5) text(x = 8, y = 55, paste("mean = ",round(m,2)), cex = 1.5) text(x = 8, y = 45, paste("sd = ",round(s,2)), cex = 1.5) ``` - Mean = 6.88 hours, SD = 0.92 hours ## Numer of hours of sleep on school nights ```{r, echo=F, message=F, warning=F, fig.width=6, fig.height=3,fig.align='center'} data(COL) par(mar = c(2.5,2.5,0,0), las = 1) hist(sleep, col = COL[1], main = "", xlab = "", ylab = "", axes = FALSE) axis(1, cex.axis = 1.5) axis(2, at = seq(0,80,20), cex.axis = 1.5) abline(v = m) rect(m-s, -5, m+s, 500, col=COL[6,4], border='#00000000') text(x = m, y = 30, paste(round(sum((sleep >= m - s) & (sleep <= m + s)) / n,2)*100,"%"), col = COL[4], cex = 1.5) lines(x = c(m-s,m-0.5),y = c(30,30), col = COL[4], lwd = 2) lines(x = c(m+0.5,m+s),y = c(30,30), col = COL[4], lwd = 2) ``` - Mean = 6.88 hours, SD = 0.92 hours - 72\% of the data are within 1 SD of the mean: 6.88 $\pm$ 0.93. ## Numer of hours of sleep on school nights ```{r, echo=F, message=F, warning=F, fig.width=6, fig.height=3,fig.align='center'} data(COL) par(mar = c(2.5,2.5,0,0), las = 1) hist(sleep, col = COL[1], main = "", xlab = "", ylab = "", axes = FALSE) axis(1, cex.axis = 1.5) axis(2, at = seq(0,80,20), cex.axis = 1.5) abline(v = m) rect(m-s, -5, m+s, 500, col=COL[6,4], border='#00000000') rect(m-2*s, -5, m+2*s, 500, col=COL[6,3], border='#00000000') text(x = m, y = 30, paste(round(sum((sleep >= m - s) & (sleep <= m + s)) / n,2)*100,"%"), col = COL[4], cex = 1.5) lines(x = c(m-s,m-0.5),y = c(30,30), col = COL[4], lwd = 2) lines(x = c(m+0.5,m+s),y = c(30,30), col = COL[4], lwd = 2) text(x = m, y = 50, paste(round(sum((sleep >= m - 2*s) & (sleep <= m + 2*s)) / n,2)*100,"%"), col = COL[4], cex = 1.5) lines(x = c(m-2*s,m-0.5),y = c(50,50), col = COL[4], lwd = 2) lines(x = c(m+0.5,m+2*s),y = c(50,50), col = COL[4], lwd = 2) ``` - Mean = 6.88 hours, SD = 0.92 hours - 72\% of the data are within 1 SD of the mean: $6.88 \pm 0.93$. - 92\% of the data are within 2 SD of the mean: $6.88 \pm 2 \times 0.93$. ## Numer of hours of sleep on school nights ```{r, echo=F, message=F, warning=F, fig.width=6, fig.height=3,fig.align='center'} data(COL) par(mar = c(2.5,2.5,0,0), las = 1) hist(sleep, col = COL[1], main = "", xlab = "", ylab = "", axes = FALSE) axis(1, cex.axis = 1.5) axis(2, at = seq(0,80,20), cex.axis = 1.5) abline(v = m) rect(m-s, -5, m+s, 500, col=COL[6,4], border='#00000000') rect(m-2*s, -5, m+2*s, 500, col=COL[6,3], border='#00000000') rect(m-3*s, -5, m+3*s, 500, col=COL[6,2], border='#00000000') text(x = m, y = 30, paste(round(sum((sleep >= m - s) & (sleep <= m + s)) / n,2)*100,"%"), col = COL[4], cex = 1.5) lines(x = c(m-s,m-0.5),y = c(30,30), col = COL[4], lwd = 2) lines(x = c(m+0.5,m+s),y = c(30,30), col = COL[4], lwd = 2) text(x = m, y = 50, paste(round(sum((sleep >= m - 2*s) & (sleep <= m + 2*s)) / n,2)*100,"%"), col = COL[4], cex = 1.5) lines(x = c(m-2*s,m-0.5),y = c(50,50), col = COL[4], lwd = 2) lines(x = c(m+0.5,m+2*s),y = c(50,50), col = COL[4], lwd = 2) text(x = m, y = 70, paste(round(sum((sleep >= m - 3*s) & (sleep <= m + 3*s)) / n,2)*100,"%"), col = COL[4], cex = 1.5) lines(x = c(m-3*s,m-0.5),y = c(70,70), col = COL[4], lwd = 2) lines(x = c(m+0.5,m+3*s),y = c(70,70), col = COL[4], lwd = 2) ``` - Mean = 6.88 hours, SD = 0.92 hours - 72\% of the data are within 1 SD of the mean: $6.88 \pm 0.93$. - 92\% of the data are within 2 SD of the mean: $6.88 \pm 2 \times 0.93$. - 99\% of the data are within 3 SD of the mean: $6.88 \pm 3 \times 0.93$. ## Practice \alert{Which of the following is \underline{false}?} A) Majority of Z scores in a right skewed distribution are negative. B) In skewed distributions the Z score of the mean might be different than 0. C) For a normal distribution, IQR is less than $2 \times SD$. D) Z scores are helpful for determining how unusual a data point is compared to the rest of the data in the distribution. ## Practice \alert{Which of the following is \underline{false}?} A) Majority of Z scores in a right skewed distribution are negative. B) \alert{In skewed distributions the Z score of the mean might be different than 0.} C) For a normal distribution, IQR is less than $2 \times SD$. D) Z scores are helpful for determining how unusual a data point is compared to the rest of the data in the distribution.