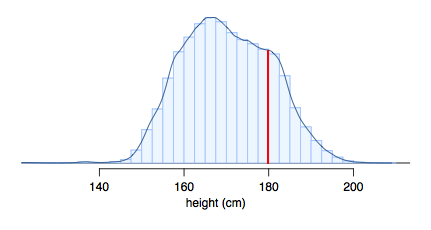
```{r setup, include=FALSE} knitr::opts_chunk$set(echo = FALSE) ``` ```{r, echo=F, message=F, warning=F} library(readr) library(openintro) data(COL) ``` # Continuous distributions ## Continuous distributions - Below is a histogram of the distribution of heights of US adults. - The proportion of data that falls in the shaded bins gives the probability that a randomly sampled US adult is between 180 cm and 185 cm (about 5'11" to 6'1")  ## From histogram to continuous distributions Since height is a continuous numerical variable, its **probability density function** is a smooth curve.  ## Probabilities from continuous distributions Therefore, the probability that a randomly sampled US adult is between 180 cm and 185 cm can also be estimated as the shaded area under the curve.  ## By definition... Since continuous probabilities are estimated as "the area under the curve", the probability of being exactly 180 cm (or any exact value) is defined as **0**.